Vjeux

I'm working a lot with URLs that contain ids and very often, I made a mistake in one digit of the long id and end up with a completely different element. If I don't pay attention, then I end up looking at two elements thinking they are the same and am intrigued until I find out the mistake.

In order to avoid that, I wanted to know if I could make a sequence of ids where making one mistake would not give a valid id. For example, if you have the id 473, then you have to black list all the ids where the first digit is wrong (073, 173, 273, 373, 573, 673, 773, 873, 973) and the second being wrong (403, 413, 423, 433, 443, 453, 463, 483, 493) and the last one (470, 471, 472, 474, 475, 476, 477, 478, 479).

Here is the list of the first pseudo-numbers:

1. 011
2. 022
3. 033
4. 044
5. 055
6. 066
7. 077
8. 088
9. 099
10. 101
11. 110
12. 123
13. 132
14. 145
15. 154
16. 167
17. 176
18. 189
19. 198
20. 202
21. 213
22. 220
23. 231
24. 246
25. 257
26. 264
27. 275
28. 303
29. 312
30. 321
31. 330
32. 347
33. 356
34. 365
35. 374
36. 404
37. 415
38. 426
39. 437
40. 440
41. 451
42. 462
43. 473
44. 505
45. 514
46. 527
47. 536
48. 541
49. 550
50. 563
51. 572
52. 606
53. 617
54. 624
55. 635
56. 642
57. 653
58. 660
59. 671
60. 707
61. 716
62. 725
63. 734
64. 743
65. 752
66. 761
67. 770
68. 808
69. 819
70. 880
71. 891
72. 909
73. 918
74. 981
75. 990

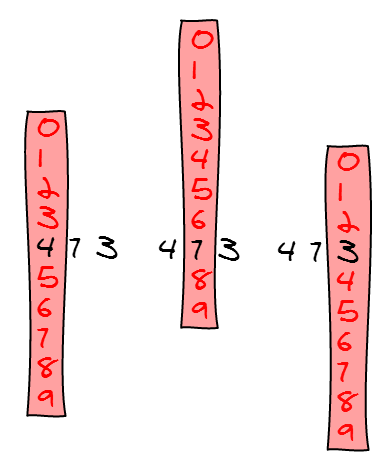
And here is a visual representation of those numbers:

For each digit in the number, we blacklist 9 other numbers. For a 5 digits number (eg 12345), that means blacklisting 45 numbers. For a 10 digits number (eg 1234567890), that means blacklisting 90 numbers. The number of blacklisted numbers only grows at a logarithmic scale.

In order to see how many numbers we lose, I plotted the ratio of pseudo numbers count compared to the real numbers. We can roughly keep one number every fifteen. But the good news is that the ratio doesn't fall off the chart as the numbers grow.

Looking at the numbers, they looked like to go from 10 to 10 but with some huge spikes and sometimes they were closer. So I plotted the difference between two consecutive numbers in a chart and it looks like the difference is centered around 10. But the variance is getting higher and higher as you move further.

I'm not really sure if this sequence can be really useful in practice but that was a fun week-end experiment. I hope it'll give you some, hopefully useful, ideas 🙂