At school we've been studying Lie Algebra and we were asked to make a 3D representation of a Lie Group. We chose to represent Julia Set in the Quaternion domain.
We were really impressed to see that it was possible to generate many different forms given such a simple equation. Feel free to share links with some cool settings in the comments 🙂
The demo has been written in WebGL using ThreeJS.
A bit of Mathematics
Les ensembles de Julia sont des fractales définies par une suite de récurrence \(z_{n+1} = z^{2}_{n} + r\). Avec \(r\) une constante. Si, pour un \(z_{0}\) fixé, \((z_{n})\) converge alors \(z_{0}\) est dans l'ensemble de Julia.
Les ensembles de Julia peuvent être représentés en 2 dimensions en prenant \(r \in \mathbb{C}\) ou alors en 4 dimensions en prenant \(r \in \mathbb{H}\). \(\mathbb{H}\) étant l'ensemble des quaternions. Les quaternions sont des nombres hypercomplexes de la forme: \[a + i \times b + j \times c + k \times d \ \ \ \ \ \ (a, b, c, d) \in \mathbb{R}\] Avec \(i\), \(j\), \(k\) des racines complexes de l'unité, c'est-à-dire: \(i^{2} = j^{2} = k^{2} = ijk = 1\).
Afin d'obtenir une représentation dans un espace à quatre dimensions on représente chaque point de cet espace par un quaternion. À \(r\) fixé on obtient l'ensemble de Julia correspondant en testant la convergence de
\((z_{n})\) pour tous les points de l'espace.
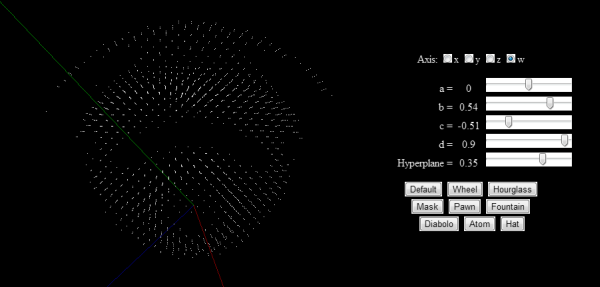
Dans notre démonstration les coefficients de la constante sont modifiables via les curseurs \(a\), \(b\), \(c\) et \(d\). Pour obtenir une représentation en 3D il est nécessaire de réaliser une coupe de l'ensemble de Julia par un hyperplan. Dans la pratique cela signifie que nous assignons une valeur constante à un même coefficient pour tous les quaternions. On assimile alors les 3 coefficients restants aux axes \(x\), \(y\) et \(z\) d'un repère 3D.
Dans notre démonstration on peut choisir quel coefficient fixer et modifier sa valeur avec le curseur Hyperplane. Une fois un coefficient fixé on fait ensuite varier \(x\), \(y\), et \(z\). Par exemple si on a fixé le coefficient de \(k\) à \(W\), la valeur initiale de la suite est donc: \(z_{0} = x + i \times y + j \times z + k \times W\).
Le point \((x, y, z)\) est alors dans l'ensemble de Julia si après un nombre fixé d'itérations la valeur de la suite n'a pas dépassé un certain seuil. Dans notre démonstration, nous avons choisi d'effectuer 10 itérations.